线性回归
简单线性回归
本章学习如何运用『 回归分析 』方法去建立模型,根据一个变量的值去预测另一个变量的值。
在数学中,『 函数关系 』指的是有两个变量 x 和 y,变量 y 随变量 x 一起变化,并完全依赖于 x,当变量 x 取某个数值时,y 依确定的关系取相应的值,记为 y=f(x) 其中 x 称为自变量,y 称为因变量。函数关系是一一对应的确定关系。
在现实生活中,很多变量之间存在某种关系,但这种关系不是函数关系,它们是一种不确定的数量关系,称为『 相关关系 』指一个变量的取值不能由另一个变量唯一确定,当变量 x 取某个值时,变量 y 的取值可能有几个。
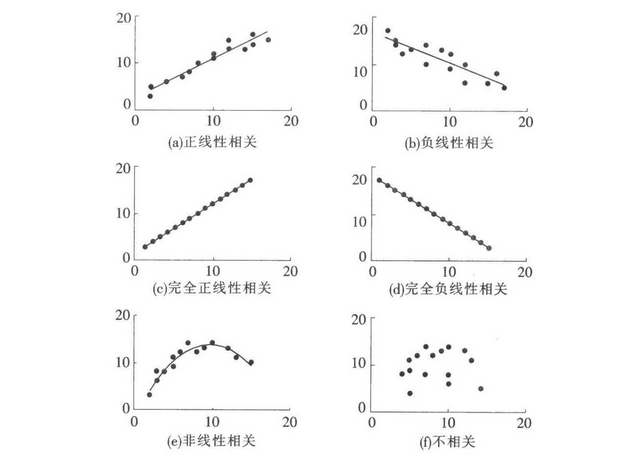
最简单的一种相关关系是『 线性相关 』,是指变量之间的关系近似地表现为一条直线。
对于具有线性关系的两个变量,可以用一个线性方程来表示它们之间的关系。描述因变量 y 如何依赖于自变量 x 和误差项 ε 的方程。对于只涉及一个自变量的『 简单 ( 一元 ) 线性回归模型 』可表示为:
Y=α+βX+ϵ - α 是 Y 轴截距 y-intercept,是 X 等于 0 时的 Y 值。
- β 是直线的斜率,表示 X 每变化一个单位,Y 的变化的量。
- X 称为自变量,Y 称为因变量。在回归分析中,想要预测的变量称为因变量,被用来预测的变量称为自变量。
- ε 表示数据点对这条直线具有一个随机的随机量。

- 误差项 ε 是一个服从正态分布的随机变量,期望值为 0,且对于所有的 x 值,ε 的方差 σ2 都相同

根据回归模型中的假定,ε 的期望值等于 0,因此 y 的期望值可以描述为一个依赖于 x 的线性函数。
描述回归模型中因变量 y 的期望值如何依赖于自变量 x 的方程称为『 回归方程 』。
对于只涉及一个自变量的线性回归方程,称为『 简单线性回归方程 』,可以表述为:
y^=a+bx - a 和 b 称为『 回归系数 』
- 在实际分析问题时,我们要解释这两个系数分别代表的具体意思。
🌰 例子:
一个数学老师把学生的 "期末考试成绩 y" 和 "复习小时数 x" 的数据输入到电脑中,希望找到这两个变量之间的关系。
得到回归方程如下:
y^=35+3x 截距 a 为 35,斜率 b 为 3。意思是,学生如果完全不复习,期末成绩为 35。如果每增加 1 小时学习时间,期末可以多考 3 分。
确定简单线性回归方程 ( 最小二乘法 )
确定 a 和 b 的值最简单的方法是用『 最小二乘法 』

在图中可以看到每个点到直线有一个垂线, 它代表点到直线的误差我们可以找到一条直线, 使得『 误差平方和 Sum of squares for error, SSE 』最小.
SSE=Σ(yi−y^i)2=Σ(yi−a−bxi)2 对于回归方程的两个回归系数 a 和 b,可以通过如下方法计算:
b=SxxSxya=yˉ−bxˉSxy=Σ(xi−xˉ)(yi−yˉ)=Σxiyi−n(Σxi)(Σyi)Sxx=Σ(xi−xˉ)2=Σxi2−n(Σxi)2 🌰 例子:
假设有如下数据,x 代表学生历史课的成绩,y 代表学生微积分的成绩。
试着找出 x 和 y 的线性方程。
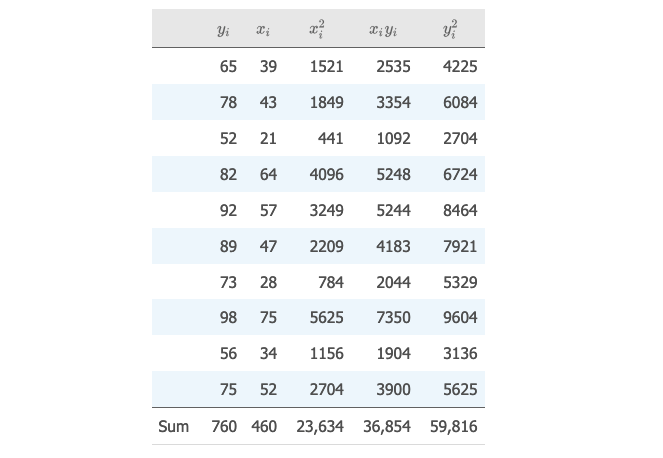
Sxx=Σxi2−n(Σxi)2=23,634−10(460)2=2474Sxy=Σxiyi−n(∑xi)(Σyi)=36,854−10(460)(760)=1894yˉ=nΣyi=10760=76xˉ=nΣxi=10460=46b=SxxSxy=24741894=0.76556a=yˉ−bxˉ=76−(0.76556)(46)=40.78424 得到一元线性回归方程:
y^=a+bx=40.78424+0.76556x 假如一个学生历史课的分数为 50,带入到方程中,可以算出来期望的微积分的分数为 79.06。
当然,通过计算机也可以帮助我们去计算这条直线。
多元线性回归




