# 参数估计 & 假设检验
前面已经介绍了很多随机变量的概率分布,和关于样本统计量的抽样分布。根据 "中心极限定理" 可知,无论总体是怎样分布的,它的样本的统计量的抽样分布都是正态的。
这一章介绍,如何去估计总体的 "参数"。
推断统计关心的就是如何去得到一个总体的 "参数",也就描述总体特性的数值描述性度量。
主要有两种方式去进行推断:
- 参数估计 Estimation:根据样本的信息去估计出总体的参数。
- 假设检验 Hypothesis Testing:先自己估计出一个可能的参数值,然后再去判断正确性。
# 参数估计
『 估计量 estimator 』是指基于样本的观测数据计算出总体参数的 "估计值 estimate" 的法则 ( 公式 )
估计量可以通过两种方式得到:点估计 & 区间估计。
# 点估计 & 区间估计
# 什么是『 点估计 』
『 点估计 point estimation 』基于样本数据,计算出"一个" 数值作为总体参数的估计值。
- 从一个样本计算出的统计量,称为『 点估计值 point estimate 』
- 样本统计量的抽样分布,称为『 点估计量 point estimator 』是一个关于估计值的函数。
如果一个参数的估计量的分布的均值与真正的参数值相同,则该估计量被称为是『 无偏的 unbiased 』。否则称为『 有偏的 biased 』
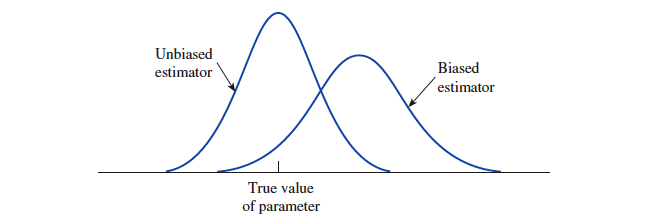
一个估计量的分布的方差应该是越小越好。越小的方差意味着真正的参数值接近于分布均值的可能性越大。
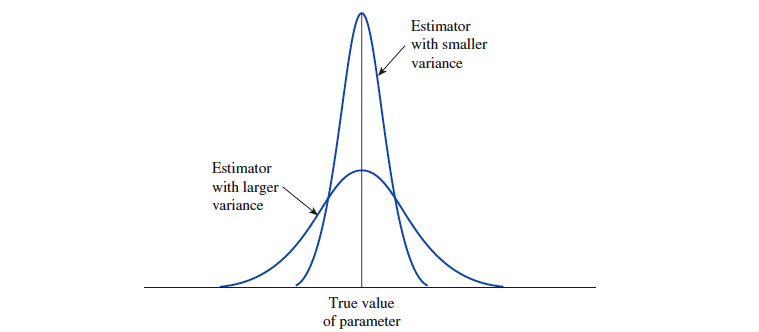
估计值与真正参数值之间的差被称为『 误差 error of estimation 』
假设样本的容量足够到,得到的估计量都是无偏的,估计量的分布都近似正态分布。根据中心极限定理可以计算出,一个估计量有 的可能性,落入估计量分布中的均值左右各 个标准误 SE 的范围内。
- 对于无偏的估计量,这就意味着一个估计值有 的可能性与参数的误差在 个标准误之内。
- 估计量均值左右各 个标准误的区间称为『 95% margin of error 』简称 "margin of error"。
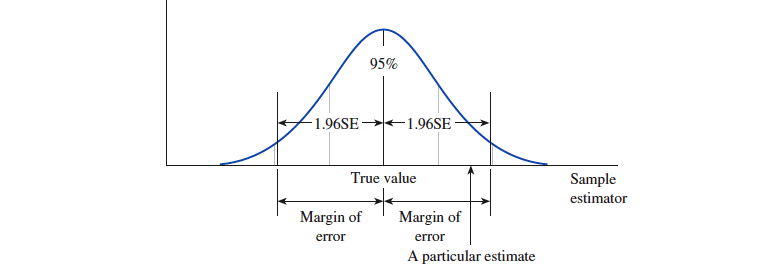
你可能发现了,估计量的 "标准误" 计算是要用到总体的标准差 的。但是我们并不知道总体的参数。所以只能用从样本中计算出的参数值 估计为总体的标准差。虽然不是很准确,但也只好如此。
🌰 例子:
电视台想知道每个人每周平均看多长时间电视。它们随机抽出了 50 个人作为样本,计算得出平均观看时长为 小时每周。标准差为 小时。
首先,将样本的标准差作为总体的标准差,计算得出估计量的标准误,并且将它乘上 :
我可以认为 有 的可能性与总体均值的距离在 小时以内。
# 什么是『 区间估计 』
『 区间估计 interval estimation 』基于样本数据,计算出 "两个" 数值去构建一个区间,总体参数的估计值可能落于其中。
- 用于计算的公式,称为『 区间估计量 interval estimator 』
- 计算出的两个数值,称为『 区间估计值 interval estimate 』根据位置又可以分别称为『 置信下限 Lower Control Limit, LCL 』和『 置信上限 Upper Control Limit, UCL 』
- 两个数值构成的区间,称为『 置信区间 confidence interval 』
- 这个区间包含被估参数的概率称为『 置信系数 confidence coefficient 』一个置信区间的置信系数为 0.95, 则称其为是 95% 的置信区间. 意思是有 95% 的可能性被估计参数落入这个区间中。
# 均值的置信区间估计 ( 大样本容量 )
现在,假设我们知道总体的标准差 。或者直接用样本的标准差作为总体标准差的估计 ( 样本容量大时 )
通过前面我们知道,从一个样本计算出的估计量,有 的几率在估计量均值左右各 个 "标准误 SE" 之内。
那么反过来说,我从总体中随机抽样,然后计算出样本的均值,在均值左右两边各 个 "标准误 SE" 位置划出一个区间。这个区间有 的几率包含 "总体的均值"。
这个区间可以称为称为置信度为 的置信区间。
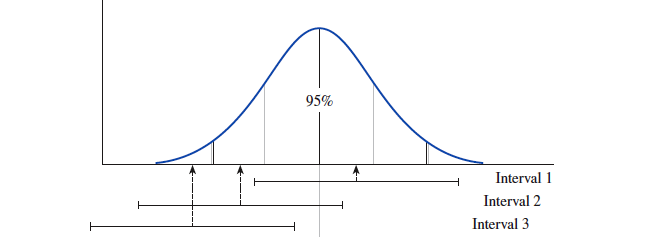
可以将统计量分布转换成标准正态分布:
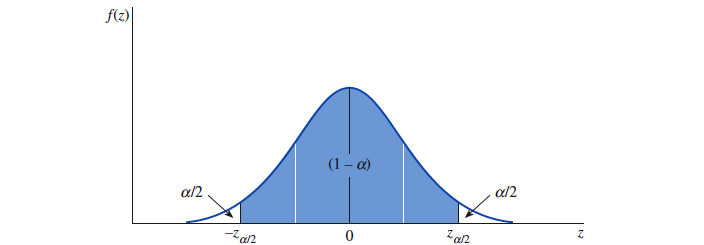
- 置信度用 表示。 为总体均值不在区间内的槪率。
- 分布的上尾和下尾面分别都是
- 置信区间为
- = 标准正态分布中对应于曲线面枳为 的值。在置信区间中, 值又称为『 临界值 critical value 』
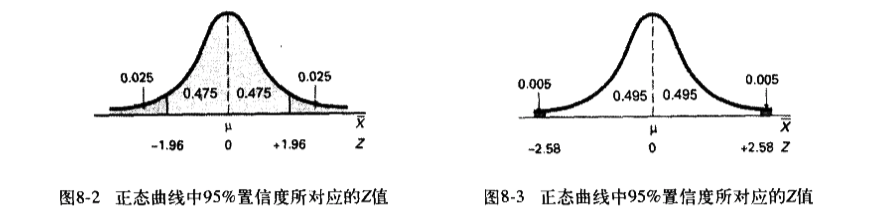
- 🌰 的置信度对应于 为 。对应于曲线面积 的 值,也就是临界值为 。
置信度可以通过增大区间范围来提高,但这也造成了区间精度的下降。
🌰 例子:
造纸厂对于每张纸的长度的期望均值是 11 英寸,标准差为 0.02 英寸。请通过抽样检验来判断产品生产是否符合预期。
现在,从成品中随机抽取 100 张纸,然后计算出样本均值 10.998 英寸。计算 95% 置信度的总体均值区间估计。
计算得到,
这个区间中包含了 11,所以证明生产流程还在正常运作。
# 均值的置信区间估计 ( 小样本容量 )
# 比例的置信区间估计
WARNING
⚠️ 建设中...
# 确定样本容量
在实际进行抽样分析之前,就需要确定好样本的容量。确定样本容量是个很复 杂的过程,受到金钱、时间、可接受误差的限制。
# 确定 "均值估计" 的样本容量
在总体均值估计的样本容量的确定中,我们先不管金钱和时间的限制。首先要确定好:
- 可以接受多大的 "抽样误差"。
- 区间估计中的 "罝信度水平"。
抽样误差,指的是在置信区间中加在样本均值两边的量,用符号 表示。
通过上面 👆 的公式我们可以得出 "样本容量" 的计算公式:
这个公式中设计 3 个变量,置信度决定了 值,可接受的抽样误差 ,总体的标准差 。
我们一般很难事先知道总体的标准差 。
- 在有些情况,可以根据以往的数据来估计标准差。
- 在其他情况下,可以用数值分布范围和变量的分布情况来估算。如果总体是正态分布,那么数值分布的范围就近似等于 。可以用取值范围除以 来求 值。
- 还可以进行小规模调査,根据调査数据来估算标准差。
🌰 例子:
一家公司想要知道所有的销售发票上金额的均值是多少。决定抽样误差小于 美元,置信度为 ,以往的记录显示标准差大约为 美元。
计算合适的抽样容量:
取一个大于计算值的整数,所以样本容量为 97。公司可能为了使用起来方便,选取 100 这个数字。
# 假设检验 ( 单样本 )
# 什么是假设检验
假设检验是一种统计推断的方法。通常是以关于总体参数的一个假设开始,然后通过分析样本数据,再去判断这个假设应该被接收还是被拒绝。
假设检验采用逻辑上的反证法,即为了检验一个假设是否成立,首先假设它是真的,然后对样本进行观察:
- 如果发现出现了不合理现象,则可以认为假设是不合理的,拒绝假设。
- 否则可以认为假设是合理的,接受假设。
- "假设不合理" 的意思是说假设正确的可能性很低,属于小概率事件。
# 原假设 & 备择假设
『 原假设 null hypothesis 』指进行统计检验时预先建立的假设,用 表示。
- 通常表示的是期望的情况。
- 假设中总是有等号,比如 或
- 注意,我们通过分析样本数据,并不能证明原假设正确与否。只能说它是正确的可能性非常大。
『 备择假设 alternative hypothesis 』指与原假设相反的假设,用 表示。
- 当备择假设是正确的时,原假设就必然是错误的。
- 永远不会表述为总体参数等于某个具体值,只可能有 或
- 同样,我们不能证明备择假设正确与否。只能说备择假设正确的可能性非常大。
🌰 例子:
你是快餐店的经营者。想要确定预定位子的等待时间在过去几个月是否改变 ,以前的总体均值是 4.5 分钟。请写出原假设和备择假设。
原假设是总体的均值没有改变、仍旧是 4.5 分钟。表述为
备择假设是原假设的对立面。因为原假设是总体均值为 4.5 分钟,所以备择假设是总体均值不是 4.5 分钟,表述如下:
# 拒绝域 & 接收域
假设检验的思路就是,根据样本得出的信息确定原假设是正确的可能性。如果原假设是正确的,你可以认为从样本计算出的统计值应该与总体参数很相近。如果差异很大,你就可以认为原假设是错误的。
我们需要一种标准去 "量化" 统计值与原假设中的参数值的差异。
如果原假设是正确的,那么样本统计量的抽样分布,应该呈现正态分布,且均值等于原假设中定义的值。
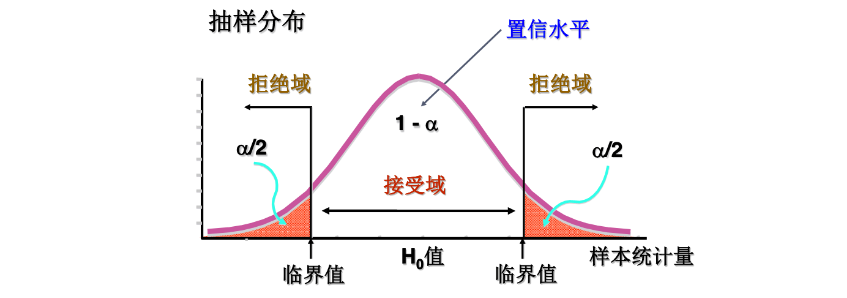
『 拒绝域 region of rejection 』如果样本的统计量落在拒绝域之内的,就要拒绝原假设。因为这些值在原假设正确时不大可能发生。
『 接受域 region of nonrejection 』如果样本的统计量落在接受域之内,就没有足够的证据证明原假设错误,就不能拒绝原假设。
『 临界值 critical value 』把接受域和拒绝域划分开来。临界值的大小取决干拒绝域的大小。
# 第 I 类错误 & 第 II 类错误
在使用假设检验时你会犯两类错误:
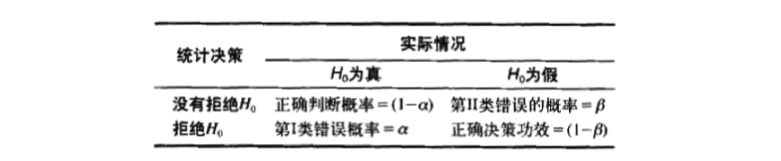
『 第 I 类错误 』你拒绝了原假设,而实际上它是正确的或不应该被拒绝的,这种类型错误的发生概率记为
- 概率 又被称为『 显著性水平 level of significance 』
- 在假设检验之前,就要确定好显著性水平。
- 通常为 0.01,0.04,0.10
- 得出一侧拒绝域的大小,进而计算出 "临界值"。
- 『 置信系数 』等于 。表示你没有拒绝原假设,同时原假设也是正确的概率。
- 当乘上 100% 时,置信系数就变成 "置信度"。
『 第 II 类错误 』你接收了原假设,但实际上它是错误的或应该被拒绝的,这种类型错误的发生概率为
- 你不能像第 I 类错误那样自己控制 的值。只能依靠假设值和实际总体参数值的差距来决定。
- 如果假设值与总体参数实际值之间的差别大,那么 就小。但是,如果假设值与总体参数实际值之间的差别很小,那么 就比较大。
- 表示你拒接了原假设,实际上原假设也是错误的概率。
- 降低 的方法之一是增大样本容量。大样本通常能使假设检验值与总体参数之间的差距非常小。
对于给定的样本容量,对 和 的选择主要还是根据这两种错误发生后的造成的代价成本来确定:
- 如果错误地 "拒绝" 原假设会造成巨大损失,那么拒绝原假设的概率 就应定的小一些。
- 如果错误地 "接受" 原假设会造成巨大损失,那么拒绝原假设的概率 就应定的大一些。
同时也要注意 和 相互的关系:
- 你可以通过选择较小的 水平来直接地降低第 I 类错误的风险。但是,当你降低 水平,就增加了 ,也就是增加了第 II 类错误发生的几率。
- 如果你希望降低 , 你可以选择较大的 ,但这也增加了第 I 类错误发生的几率。
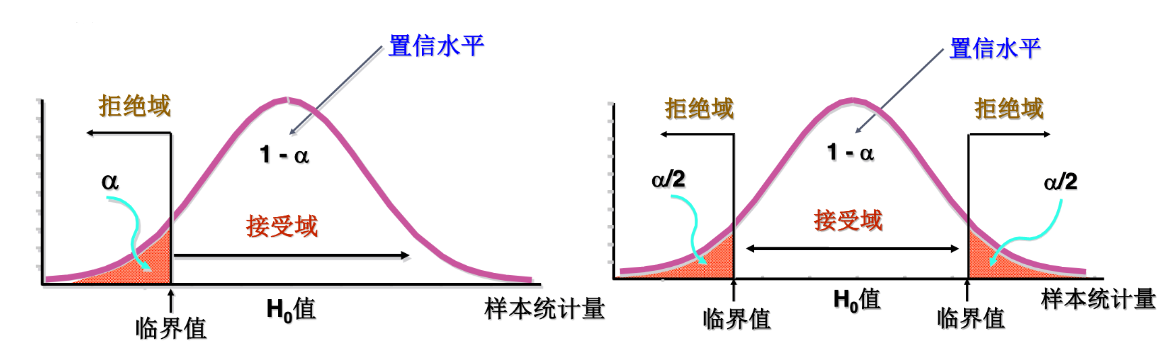
# 双侧检测 & 单侧检测
『 双侧检测 』有两个临界值,两个拒绝域,每个拒绝域的面积为 。
『 单侧检测 』只有一个临界值,一个拒绝域,拒绝域的面积为 。
- 很多时候,假设检验只关心某一单边的情况。
- 🌰 例如,判断生产食品的平均重量是否低于一个假设值。
# 置信区间 & 假设检验的关系
# 均值的假设检验
# 已知, 检验
在 是已知的情况下,的可以运用 得分去度量样本均值和总体均值 之间的差异。
假设检验的 6 步法:
- 写出原假设 ,备择假设 。
- 选择显著性水平 ,及样本容量 。显著性水平是根据问題中犯第 I 类错误和第 II 类错误的风险 的相对重要性来确定的。
- 确定合适的检验统计量及抽样分布。
- 确定划分拒绝域和接受域的临界值。
- 收集样本数据计算检验统计量的值。
- 给出统计学意义上的结论。如果检验统计值是落在接受区域的,你就不能拒绝原假设。如果检验统计值落在拒绝区域内,就可以拒绝原假设。
🌰 例子:
一个食品工厂生产的一袋食品预期平均重量为 。现在随机抽出一批成品,进行假设检验,判断是否生产出的食品重量符合预期。
- 定义假设:
选择显著性水平和样本容量:
- 在这个例题中,第 I 类错误认为总体均值不为 368 克,而实际上是 368 克。错误发生后,工厂可能会对生产流程做校正措施。这会花费大量无意义的金钱和时间。所以应该尽量避免第 I 类错误发生。
- 应该使 尽量小一些,让第 I 类错误发生概率变小。
- 选择 。样本容量 。
逸择合适的检验统计量:
- 因为 是已知的,你可以运用服从正态分布 的 Z 检验统计量。
确定临界值:
- 因为 所以 ,在标准正态分布中,计算得出对应的 值为 。
收集样本数据:
- 假设,根据样本数据计算得出的均值的检验统计量值为
给出统计学意义上的结论:
- 是在接受域之内,因为 且 。统计意义上的决定是接受原假设 ,包装流程不需要进行校正。
🌰 例子:
一家加工干 奶酪的公司关注的是某些供应商提供的牛奶是否兑水,太多的水会降低牛奶的凝固点。天然牛奶的凝固点服从正态分布,其均值是 ,天然牛奶的凝固点的标准差是 。
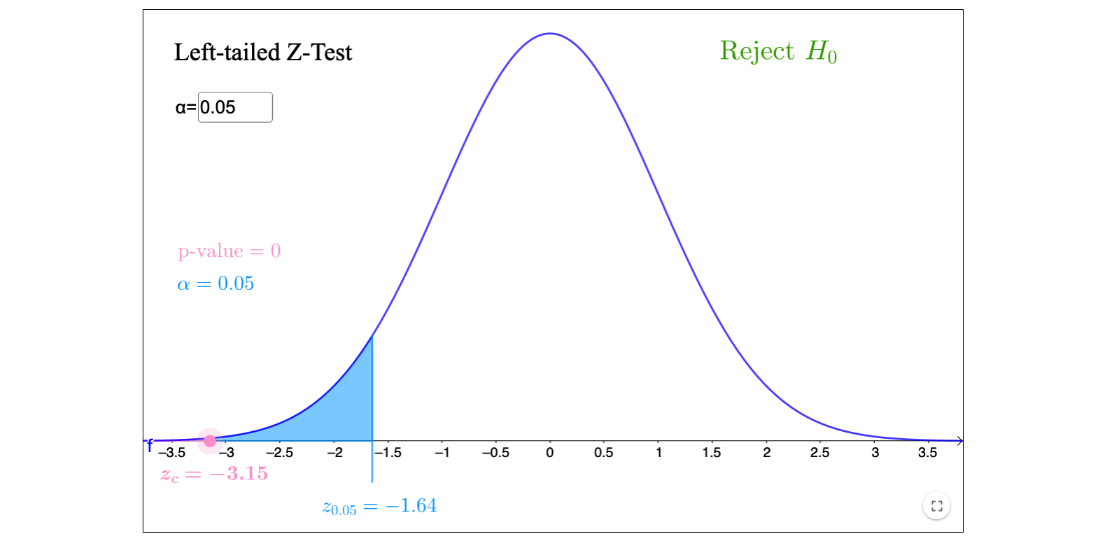
因为奶酪生产公司关心的只是确定牛奶的凝固点是否低于天然牛奶的平均温度,所以整个拒绝域就是在抽样分布的左边,属于单边检测。
定义假设:
你选择样本容 ,决定使用 。计算得到对应的临界值为
因为 是已知的,所以你要用服从正态分布 检验统计量。
随机抽取了 箱牛奶的样本,计算得出样本均值的凝固点等于 。计算得到对应的 得分为
因为 ,所以要拒绝原假设。结论是供应的牛奶的平均凝固点低于 ,很有可能牛奶兑水了。
# 未知, 检验
在很多关于总体均值的假设检验中,你并不知道总体标准差。此时,你要使用样本标准差 。如果你假设总体服从正态分布,样本均值的抽样分布服从自由度为 的 分布。
如果总体不是服从正态分布,你同样可以用 检验,因为只要样本容量足够大,根据中心极限定理可知,样本均值的抽样分布趋近 分布。