# 离散概率
# 离散概率引论
# 有限概率

定义:


例子:


# 事件组合的概率
定理:

例子:

定理:

例子:

# 概率的推理
一个常见的问题是确定两个事件中的哪一个更有可能发生,分析这些事件的概率可能比较复杂。
例子:

# 概率论
# 概率指派

定义:

例子:


例子:


# 事件的组合

定理:

# 条件概率

定义:
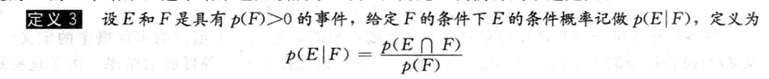
例子:

# 独立性

定义:
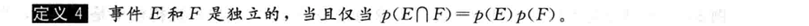
例子:

定义:

# 伯努利试验 & 二项分布
# 伯努利试验


定理:

例子:

# 二项分布

例子:


# 随机变量

定义:

例子:
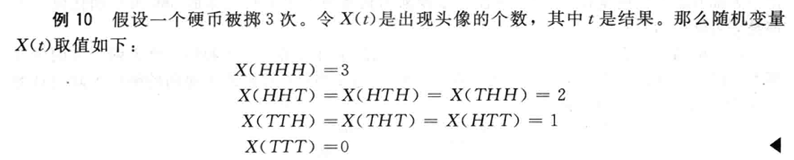
定义:

例子:

# 生日问题

# 蒙特卡罗算法
至今讨论的算法都是确定性算法。即只要给定同样的输入,每个算法总是以同样的方式运行。但是有许多情况下我们希望算法在一步或多步中做随机选择。当一个确定性算法不得不遇到大量的甚至是无数种可能的情况时就会出现这种情况。在一步或者多步做随机选择的算法称为概率算法。
这一节我们将讨论关于判定问题的一类特殊的概率算法,即蒙特卡罗算法。蒙特卡罗算法对于问题总能得到答案,但是这些答案可能存在很小的出错概率。当算法执行足够多的计算时,答案出错的概率迅速下降。判定问题以“真”或者“假”作为它们的答案。“蒙特卡罗”是摩纳哥的一个著名赌场。

例子:


# 概率方法
定理:


定理:


# 贝叶斯定理
# 贝叶斯定理介绍
定义:



例子:


例子:

# 贝叶斯垃圾邮件过滤器


例子:
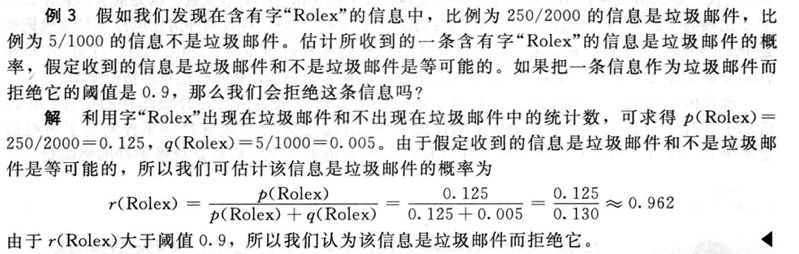

例子:



# 期望值 & 方差


# 期望值
定义:

例子:


定理:

例子:

定理:

# 期望的线性性质
定理:



例子:

例子:

# 平均情形下的计算复杂度

例子:


# 几何分布
定义:

例子:


# 独立随机变量
定义:
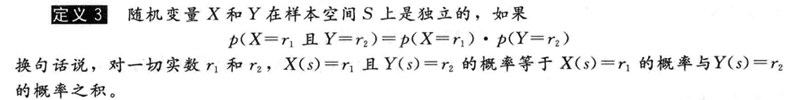
例子:

定理:
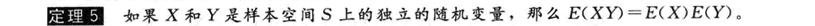

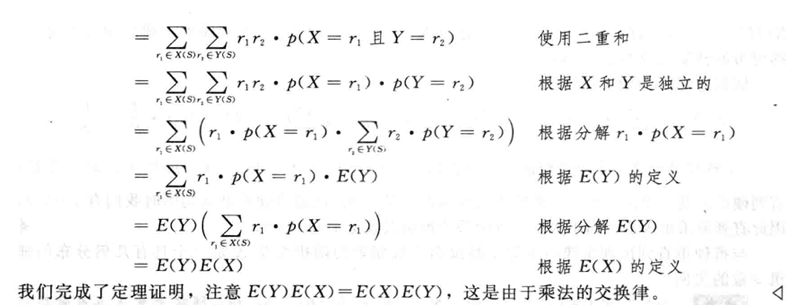
例子:

# 方差

定义:
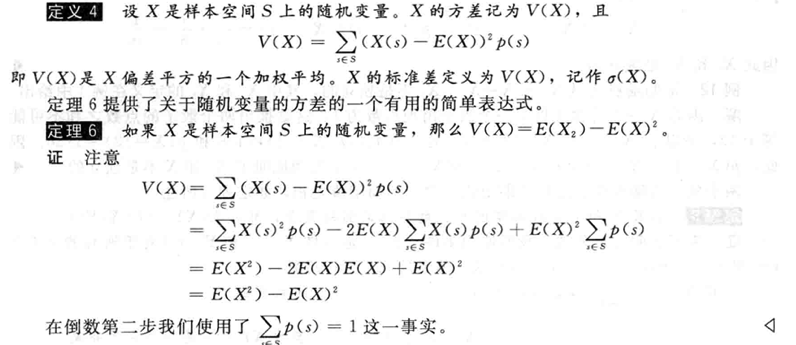
推论:


例子:


定理:

例子:


# 切比雪夫不等式

定理:

例子:
